SCI/FreeSCI/Pathfinding/Specification
Specification
In this section we give a formal specification of the AvoidPath kernel function.
This function computes a path from a start point to an end point, avoiding a set of polygons. We start out by formalizing the main notions from Sierra's pathfinding patent section.
A point v is a position in the plane. Let x(v) denote the x–coordinate of v and y(v) the y–coordinate of v.
A path is a list of points (v0 , …, vn ) and a polygon is a closed path. We now define the near point:
- Definition 1
- Let P be a polygon and p be a point. Let E be the set of edges of P that do not lie along the display border. The near point of p is a point at minimal distance from p that lies on an edge in E.
- There are four different types of polygons, as described in Polygon types section. We now formalize the constraints the polygon types impose on the path that is to be computed. We start with the barred access polygon. If the start point is contained in the polygon we use the semantics used by later versions of Sierra SCI, i.e . the path must leave the polygon immediately via the near point. This way the traversal through the polygon is minimal.
- Definition 2
- Let P be a barred access polygon. If the start point s is contained in P the path must immediately exit the polygon via the near point of s. Except for that edge, the path may not intersect the inside of P. If the end point t is contained in P the path must end at the near point of t, instead of t.
- For the total and near-point access polygons the definitions are straightforward.
- Definition 3
- Let P be a total access polygon. The path may not intersect the inside of P unless the start or end point is contained in P.
- Definition 4
- Let P be a near-point access polygon. If the start point s is contained in P the path must immediately exit the polygon via the near point of s.
- Similarly, if the end point t is contained in P the path must reach t via the near point of t. Except for those edges, the path may not intersect the inside of P.
It was not possible to test the contained access polygon type with the experimentator, so the exact semantics are unknown. However, this polygon is intuitively similar to the barred access polygon, except that instead of the inside of the polygon it is the outside that cannot be entered. We assume that the semantics of contained access polygon are analogous to those of the barred access polygon.
- Definition 5
- Let P be a contained access polygon. If the start point s is not contained in P the path must immediately enter the polygon via the near point of s. Except for that edge, the path may not intersect the outside of P. If the end point t is not contained in P the path must end at the near point of t, instead of t.
- With the addition of the contained access polygon it is no longer the case that the inside of the polygon constitutes the obstacle. We therefore define the barred area of a polygon as follows:
- Definition 6
- Let P be a polygon. If P is a contained access polygon then the barred area of P consists of the edges of P and the area outside of P. If P is not a contained access polygon then the barred area of P consists of the edges of P and the area inside of P.
- We proceed by formalizing the two assumptions from Polygon types section.
- Assumption 1
- All polygons in the polygon set are not self-intersecting.
- Assumption 2
- Let S be the polygon set. For all points p there is at most one polygon P in S for which p is contained in the barred area of P.
- We now specify the sub-functions of AvoidPath. The first sub-function is Contained.
- Specification 1 CONTAINED(v, P )
- Input:
- Apointv
- ApolygonP
- Output: true when v is contained in P, false otherwise.
- The second sub-function is ShortestPath. In order to get the desired display border semantics from Section 3.3, we define the distance from point s to point t to be infinity if t lies along the display border. We make an exception for the case where t is the end point, as the border should be reachable if the user specifically directs Ego to the display border.
- Definition 7
- Let s and t be points. If t does not lie along the display border and t is not the end point then the distance from s to t is the euclidean distance between s and t. Otherwise the distance is ∞.
- The specification of ShortestPath is as follows:
- Specification 2 ShortestPath(s, t, S)
- Input:
- A start point s
- An end point t
- A polygon set S
- Output: A shortest path from s to t that does not violate the constraints imposed by any polygon in S.
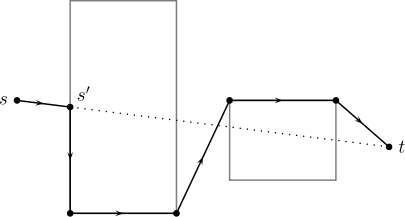
- The third sub-function KeyboardPath computes a path for keyboard support. This is not a true sub-function of AvoidPath, but we treat it as such to simplify our presentation. The semantics are described in Section 3.2. As computing the entire path as in Figure 1 would be in conflict with claim 6 of the patent, we are forced to change the semantics. Instead of using the patented method, we only compute the first edge of this path and use ShortestPath for the remainder of the path.
- As the games only use the first edge this works fine in practice. This first edge ends in what we call the blocking point.
- It is tempting to define the blocking point as the first intersection that is encountered when travelling the direct trajectory from start point to end point.
- However, this would not work correctly as the polygon edges are valid positions for Ego. If Ego tries to move away from a polygon edge the first intersection will be at the start point. With that intersection as the blocking point Ego would not move. We solve this issue by defining the blocking point as follows:
- Definition 8
- Let S be the polygon set. Let s be the start point and t be the end point. Let I be the set of intersection points of the line (s, t) and the polygons in S. The blocking point of (s, t) wrt S is the point p ∈ I closest to s for which the line (t, p) intersects the inside of the polygon at p.
- Figure 11 shows an example of a path computed by this sub-function. The blocking point s′ is determined and then ShortestPath is used to compute the portion of the path from s′ to t. This leads to the following specification:
- Specification 3 KeyboardPath(s, t, S)
- Input:
- A start point s
- An end point t
- A polygon set S.
- Let S′ be S with all total access polygons removed and all near-point access polygons changed into total access polygons.
- Output when no blocking point exists:
- The path (s, t)
- Output when there exists a blocking point s′ :
- The path concat((s), ShortestPath(s′,t,S))